

Solution: When the force ceases to act, the body will move with a constant velocity. The force then ceases to act and the body moves through 4m in the next one second. (c) From the answers in (a) and (b), what is the relationship between the time of impact and the impulsive force?Įxample 3. A force acts for 0.2 s on a body of mass 2.5 kg initially at rest. What is the impulsive force exerted on the rock? However, due to the rigidity of the rock, the time which the foot acts on the rock is only 0.01 s. (b) The boy then kicks a rock of the same mass and it moves from rest to 15 m s -1. Calculate the impulsive force exerted on the ball. (a) From Figure, when the boy kicks the 1.2 kg football, it moves from rest to 15 m s -1 in 0.1 s. Figure shows a boy kicking a football and a rock. (The negative sign shows that the force is acting against the initial direction of motion of the ball)Įxample 2. (b) the impulsive force exerted on the ball by the hands. The time of contact between the hand and the ball is 0.05 s. Figure shows the magnitudes of its velocity before and after being hit respectively. A boy hits a 0.50 kg ball and sends it moving in the opposite direction. Impulse of Force Example Problems with SolutionsĮxample 1. By doing so he increases the time interval to reduce the momentum of the ball. Cricket ball coming towards fielder has a large momentum.

Hence, impulsive force is defined as the rate of change of momentum.Įxample: While catching a cricket ball a player moves his hands backwards.The force is known as the impulsive force. Impulse is a vector quantity and has the same direction as the applied force.The SI unit for impulse is newton seconds (N s).The quantity (Force x Time) is called the impulse of a force.If a force F is applied on a body of mass m for a time interval Δt and if the change in velocity is Δv then Or force is equal to the rate of change of momentum. Since (mv – mu) is the change of momentum, therefore, By definition, acceleration, a is the rate of change in velocity and is given by the formula: When a net force acts on a body, it accelerates in the direction of the force. The change of the club's momentum divided by its collision time would give me a negative force.From the previous section, you have seen that Newtons Second Law can be summed up by the formula F = ma.

) but this is a large amount of force, and while I'm not a golfer, it seems like this is an excessive amount of force for the golfer to withstand.ĮDIT: I read this statement which sort of made it clear to me: The average force on an object during a collision is the change in the objects momentum divided by the collision time. But does this relation really hold when you examine forces? The club applies 16719.175 Newtons of Force on the ball, (and my assumption from action-reaction pairs is that that the ball, via your hint, is that the ball will exert a force of -16719.175N on the club.
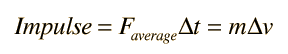
The reason the ball goes much farther is because it has to have a much larger velocity to compensate for its smaller mass relative to the club. Yes by the conservation of momentum if you add up the momentum of the club and the ball it will equal 0. For every action there is an equal and opposite reaction.īut this doesn't seem to make conceptual sense to me. My guess is you are referencing the third law: III. I found the three laws of Newton on a neat website (and am going to print them out and post it on my wall!). The question asks what the average force exerted by the club onto the ball is. Throughout the equation you were (correctly) calculating from the point of view of the ball (using the ball's mass, velocities, etc.). M * Impact speed^2 / 2*change in collision distance (b) Fave = M * Impact speed / 2 * change in collision distance / impact speed = I just assumed it was 0 m/s (when the ball would eventually come to rest) but I have a few doubts about whether this is what I am to do. Where I am getting tripped up in is what the final velocity of the ball should be. I have a feeling this is wrong because the Force should not be negative. = Pfinal - Pinitial / impact time = mVf - mVi / impact time = m(Vf - Vi)/impact time Initial velocity of golf ball: 60.797 m/sįave = change in momentum (impulse) / impact time.
CALCULATION AVERAGE IMPULSIVE FORCE MOVIE
Calculate Average Force by finding Impulse over Impact TimeĪ movie depicting a 55-g golf ball hit with a club shows that the impulse time between the club and the ball is 0.2 ms, and the initial speed of the ball is 136 mph.Ī) What is the average force exerted by the club on the ball during impact?ī) Estimate the distance over which the club and the ball are in contact during the swing.įirst converted everything to SI units.


 0 kommentar(er)
0 kommentar(er)
